
"But let her raise herself in pride! Let her follow me in my way! Let her work the work of wickedness! Let her kill her heart! Let her be loud and adulterous! Let her be covered with jewels, and rich garments, and let her be shameless before all men!"
"Then will I lift her to pinnacles of power: then will I breed from her a child mightier than all the kings of the earth. I will fill her with joy: with my force shall she see & strike at the worship of Nu: she shall achieve Hadit."
BL. III. 44 & 45

Between 2700BC to 2300BC in Sexagesimal Digits
Between 2700bc to 2300 bc, the Sumerians used the first abacus to count. It is the belief that Old Babylonians have used this abacus to do addition and subtraction.
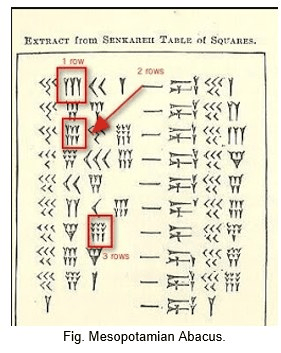
Old Babylonian scholars such as Curricio believe that the old Babylonian used their sexagesimal number system in Abacus to calculate.
Each sexagesimal digit was constituted by a series of vertical impressions of the edge of a reed stylus on the fresh clay tablet with unit value, and impressions made with the stylus turned 45 degrees or more in an anticlockwise direction of value 10.
The Decimal number 1547 is expressed in sexagesimal in the form 25:47, where "25" and "47" are two sexagesimal digits.
WiKi: Sexagesimal, also known as base 60 or sexagenary, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form—for measuring time, angles, and geographic coordinates.
The number 60, a superior highly composite number, has twelve factors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, and 60, of which 2, 3, and 5 are prime numbers. With so many factors, many fractions involving sexagesimal numbers are simplified. For example, one hour can be divided evenly into sections of 30 minutes, 20 minutes, 15 minutes, 12 minutes, 10 minutes, 6 minutes, 5 minutes, 4 minutes, 3 minutes, 2 minutes, and 1 minute. 60 is the smallest number that is divisible by every number from 1 to 6; that is, it is the lowest common multiple of 1, 2, 3, 4, 5, and 6.

In this article, all sexagesimal digits are represented as decimal numbers, except where otherwise noted. For example the largest sexagesimal digit is "59".
George, not Plimpton 322
Plimpton 322, the tablet in question, is certainly an alluring artifact. It’s a broken piece of clay roughly the size of a postcard. It was filled with four columns of cuneiform numbers around 1800 BCE, probably in the ancient city of Larsa (now in Iraq) and was removed in the 1920s.
George Plimpton bought it in 1922 and bequeathed it to Columbia University, which has owned it since 1936. Since then, many scholars have studied Plimpton 322, so any picture you might have of Mansfield and Wildberger on their hands and knees in a hot, dusty archaeological site, or even rummaging through musty, neglected archives and unearthing this treasure is inaccurate. We’ve known about the artifact and what was on it for decades. The researchers claim to have a new interpretation of how the artifact was used, but some remain skeptical.

Scholars have known since the 1940s that Plimpton 322 contains numbers involved in Pythagorean triples, that is, integer solutions to the equation a2+b2=c2. For example, 3-4-5 is a Pythagorean triple because 32+42=9+16=25=52.
The far right column consists of the numbers 1 through 15, so it’s just an enumeration. The two middle columns of Plimpton 322 contain one side and the hypotenuse of a Pythagorean triangle, or a and c in the equation a2+b2=c2. (Note that a and b are interchangeable.) But these are a little brawnier than the Pythagorean triples you learn in school. The first entries are 119 and 169, corresponding to the Pythagorean triple 1192+1202=1692. The far left column is a ratio of squares of the sides of the triangles. Exactly which sides depends slightly on what is contained in the missing shard from the left side of the artifact, but it doesn’t make a huge difference. It’s either the square of the hypotenuse divided by the square of the remaining leg or the square of one leg divided by the square of the other leg. In modern mathematical jargon, these are squares of either the tangent or the secant of an angle in the triangle.
It continues ..
One eighth equals seven and thirty in this strange base 60 world